Comparatif de performance de fonctions pour calculer la distance de Levenshtein avec un seuil

Date de publication : 18/06/2022

Ce benchmark fait suite au tutoriel Création d'une fonction pour évaluer la distance de Levenshtein avec un seuil.

Maintenant que l'on sait que les fonctions donnent le même résultat que la fonction originale, nous allons pourvoir tester et comparer leur vitesse d'exécution.

Pour cela, on utilise la librairie criterion

Implémentation

Pour commencer, nous allons créer un générateur de couplet de mots à comparer.

Nous allons réutiliser le précédent générateur genWord en l'intégrant dans un générateur qui inclut un critère sur la distance de levenshtein entre les deux mots générés.

Cela permettra de forcer le générateur à générer des couplets avec une distance précise ou minimum.

genWords tst (lmin1, lmax1) (lmin2, lmax2) = do
    w1 <- generate $ genWord lmin1 lmax1
    w2 <- generate $ genWord lmin2 lmax2
    if tst (levenshtein w1 w2)
        then return (w1, w2)
        else genWords tst (lmin1, lmax1) (lmin2, lmax2)

Nous allons ensuite créer les benchmarks à réaliser.

Nous allons commencer par comparer les deux fonctions avec différentes longueurs de mots et avec différentes valeurs seuil. Pour chaque longueur de mot, on testera la fonction levenshtein pour avoir un point de comparaison.

main = do
    defaultMainWith
        myConfig { reportFile = Just "report-leven1.html", csvFile = Just "report-leven1.csv" }
        (map
            (\(sizl, sizu) -> do
                bgroup ("Words l=" ++ show sizl ++ "-" ++ show sizu)
                    $  concatMap
                           (\m ->
                               [ (env
                                     (genWords (>= (ceiling (2 / 3 * fromIntegral (min sizl sizu))))
                                               (sizl, sizl)
                                               (sizu, sizu)
                                     )
                                     (\wrds -> bench ("levenshteinMax (" ++ show m ++ ")")
                                         $ nf (\(a, b) -> levenshteinMax m a b) wrds
                                     )
                                 )
                               , (env
                                     (genWords (>= (ceiling (2 / 3 * fromIntegral (min sizl sizu))))
                                               (sizl, sizl)
                                               (sizu, sizu)
                                     )
                                     (\wrds -> bench ("levenshteinMaxO (" ++ show m ++ ")")
                                         $ nf (\(a, b) -> levenshteinMaxO m a b) wrds
                                     )
                                 )
                               ]
                           )
                           [1 .. (ceiling (2 / 3 * fromIntegral (min sizl sizu)))]
                    ++ [ env
                             (genWords (>= (ceiling (2 / 3 * fromIntegral (min sizl sizu)))) (sizl, sizl) (sizu, sizu))
                             (\wrds -> bench ("levenshtein") $ nf (\(a, b) -> levenshtein a b) wrds)
                       ]
            )
            [(6, 6), (8, 8), (10, 10), (12, 12), (14, 14), (16, 16), (18, 18), (20, 20), (22, 22)]
        )

On crée un map avec les différentes tailles de mots à générer qui contient le test de la fonction levenshtein et un autre map avec les différentes valeurs seuil pour les tests des fonctions levenshteinMax et levenshteinMaxO.

Les valeurs seuils seront comprises entre 1 et 2/3 de la taille maximum des mots.

Les générateurs de mots seront paramétrés pour générer des couples avec une distance de levenshtein d'au moins 2/3 de la taille maximum des mots. Cela permettra d'avoir un test homogène avec des mots suffisamment différents pour ne pas fausser le test.

Maintenant que tout est en place, il ne nous reste plus qu'à compiler le fichier source avec toutes les optimisations activées. Le fichier source complet peut être trouvé ici

ghc -O2 BenchLevenshtein.hs

et de lancer le test:

./BenchLevenshtein.hs

Résultats

Petite précision concernant le dépouillement des résultats. J'ai développé les fonctions seuillées pour pouvoir discriminer rapidement des mots avec 3/4 caractères de différence, pas au delà et comme le montre les diagrammes ci-dessous donnés par criterion, au delà d'une certaine limite (environ la moitié de la longueur du mot) les fonctions seuillées sont plus lentes que la fonction originale. Les analyses se porteront donc uniquement sur des différences (seuils) allant de 1 à 4.

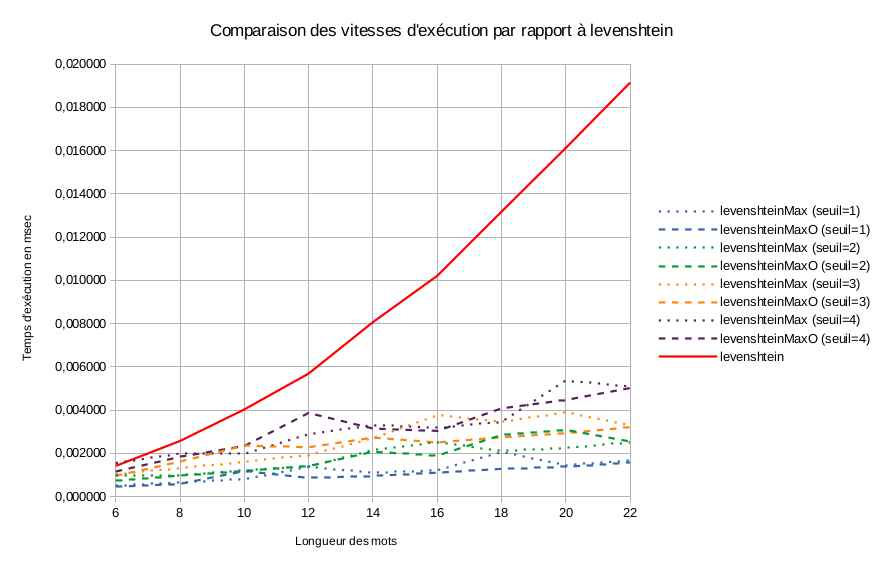
Le graphique suivant reprend les résultats donnés par le test:

La première chose que l'on remarque c'est que la vitesse de calcul de la distance de Levenshtein n'est pas proportionnelle à la longueur des mots mais exponentielle. Ce qui me conforte dans le choix de développer une version avec un seuil.

La deuxième chose que l'on remarque c'est qu'il a bien un gain par rapport à la fonction levenshtein et que plus la longueur des mots augmente, plus le gain augmente. Ce qui correspond bien à ce que l'on attendait. Ce gain peut aller de 25% avec un seuil de 3 et des mots d'une longueur de 6 caractères jusqu'à 90% avec un seuil de 1 pour une longueur de 18/22 caractères.

On remarque également que la version optimisée levenshteinMaxO apporte des gains dans certaines situations (de 1% à 30%), mais ce n'est pas toujours le cas. Dans 1/3 des cas, la version optimisée donne des performances moins bonnes que celle de la version normale (de 1% à 45%). Il est donc compliqué de pouvoir trancher sur l'intérêt de la version optimisée, d'autant que je ne peux pas expliquer ces différences de performances.

La mise au point d'une version seuillée de la distance de Levenshtein avec Haskell n'était donc pas une perte de temps et les premiers tests avec la liste de mots de mon lexique permettent un gain de temps significatif (jusqu'à 30/45 minutes !).

J'espère que ce tutoriel et que ce benchmark vous auront été utile et vous dit à très bientôt